ベイズ統計等に基づく柔らかいデータ解析

相転移現象の一種である臨界現象においてはスケーリング解析が普遍性を抽出する手法として定着していますが、従来よく用いられている最小二乗法の枠組みではうまく解析できない場合が多くあります。スケーリング則は未知のスケーリング関数を含んだ物理では珍しい緩い物理法則だからです。そのようなデータを解析するためには、ベイズ統計等に基づく最近発展しつつある柔軟な統計手法の活用が有望と考えられています。

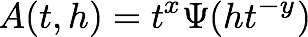
スケーリング則は物理現象だけでなく、社会現象など様々な臨界的な現象に多く現れ、重要な法則となっています。そこで、我々は、例えば、スケーリング解析におけるカーネル法などの新しい統計処理手法を持ち込む試みを展開しています。

下の動画は2次元イジングモデルの臨界点付近のビンダー比という量の有限サイズスケーリング解析の様子で、モンテカルロ法で得られたデータから臨界指数1/νや臨界温度Tc、スケーリング関数（水色の曲線）を推定しています。これらの最適なものを探索しているところを動画にしています。

助教　原田 健自

計算物理の深化と展開 沢山からできている世界を計算する：モンテカルロ法とテンソルネットワーク 量子物性 非平衡揺らぎ ベイズ統計等に基づく柔らかいデータ解析