Our group carries out theoretical research on complex systems.
The field of complex systems theory is concerned with mathematically elucidating complex behavior and high-level functioning exhibited by systems composed of many simple elements. A hallmark of the systems we study is that their complex behavior could not be anticipated from consideration of their constituent elements individually; this behavior emerges only as a manifestation of the interactions of many such elements.
For example, neuronal systems composed of many individual neurons can — through the interactions of these simple elements — come to possess such high-level information processing functions as learning, memory, recognition and decision making. These and other complex systems, for example, the Internet and transportation networks, develop autonomously and can acquire highly refined functions and great adaptability in dealing with disorders, obstacles and an evolving environment.
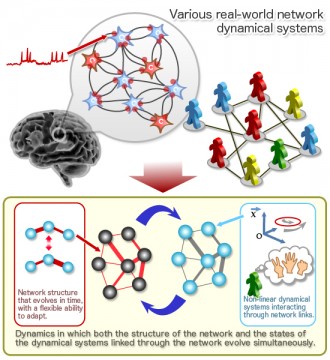
From a more general point of view, the type of systems we consider consist of many dynamic elements (for example, neurons, cities, people) that interact to form networks (neural synapses, transportation networks, friendship networks). Such systems in which these elements and the network structures through which they are connected evolve simultaneously constitute self-organizing networks.
Our group studies the cooperative behavior exhibited within such network systems formed from many interacting elements in many contexts, using the methods of non-linear dynamics and non-equilibrium statistical mechanics.
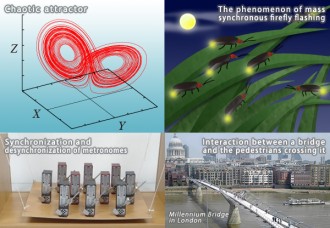
In the field of complex systems, rhythm phenomena is also an important topic. The simplest type of rhythmic behavior is the fixed rhythm exhibited by a periodic oscillator. More complex rhythmic behavior is found in many contexts. Such phenomena are important in, for example, information processing in the brain and other phenomena exhibited by living systems. And rhythm phenomena are found in even more complex forms. In fact, some types of chaos exhibit certain forms of rhythmic behavior.
In complex systems, the modeling of such phenomena as transitions involving the synchronization and desynchronization of many rhythms is an important topic of research. Also, in recent years there have been efforts to identify the nature of dynamical systems exhibiting rhythm phenomena on the basis of experimental data.
The specific research topics currently being investigated by our members are listed below. For detailed explanations, please click on each.
