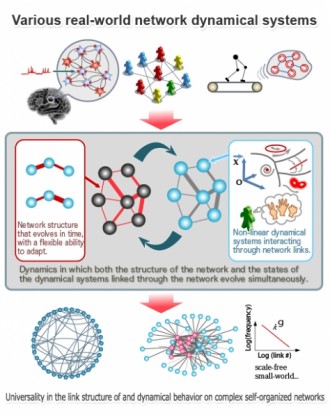
The diverse types of networks we see in the world, for example, the neural networks composing brains, social networks and transportation networks, appear on the surface to be quite different, but, in fact, there are certain types of universal structure that can be observed across such systems.
For example, the “small world” phenomenon (a manifestation of the idea that the social separations among people are small and that we are all within “six degrees of separation”) and scale-free phenomena (i.e., phenomena in which there exists no special scale) are types of universally observed characteristic phenomena. It is believed that such phenomena emerge in the form of universal structures that are realized asymptotically when each of these diverse types of networks evolves according to its own distinctive form of dynamics.
We believe that the existence of such invariant structures, i.e., the fact that there exists a common mathematical structure characterizing many different types of systems, suggests that underlying these diverse systems, there exists a universal mechanism that can be described with a common mathematical model. If we can discover such a model, its analysis should provide a new theoretical means for understanding the behavior of network systems in a unified manner.
We can regard a certain class of actual systems existing on a network as a linked dynamical system consisting of a collection of connected dynamic elements that act to alter their mutual connectivity while themselves evolving in time. Neuronal networks represent one such example.
In that case, neurons act as the fundamental elements, and they interact through the synaptic structure that they themselves create through their interaction. Then, through such interactions among many neurons, the brain acquires a high-level functioning capability.
An essential point here is that the state of each element is determined dynamically, in a manner that depends on the network structure, while simultaneously, the state of each element influences the evolution of the network structure. Each fundamental element itself possesses a type of intrinsic dynamics, and the network that couples them evolves along with the states of these individual elements. Through this type of interaction, the system as a whole comes to obtain a high-level functionality and an ability to adapt in a flexible manner.
Elucidating the essential mechanisms at work in such systems should be useful not only for scientific reasons, but also for practical reasons. For example, such knowledge could be applied for the purpose of designing networks that are stable and robust with respect to perturbations and that possess the ability to adapt to an ever-changing environment.
We are conducting interdisciplinary research aimed at understanding the universal characteristics displayed by network systems. Presently, this is being done in a somewhat abstract manner, employing models consisting of linked dynamical systems and seeking the general characteristics of the dynamics of the time-dependent network structure and the elemental states existing on this structure.
|
|