脳神経系などの生命システムやソーシャルメディアや交通網などの社会システムは、一見互いに全く違った様相に見えますが、これらの間には、共通する不変構造が隠れている場合があります。
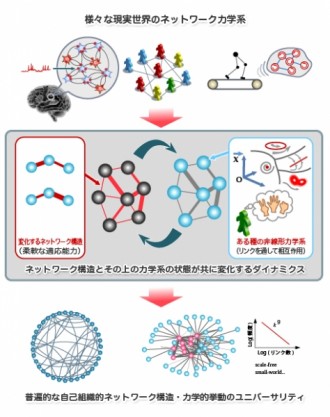
例えば、スモールワールド（世界中の人と6人の友人でつながる）やスケールフリー（特徴的なスケールがない！）などのネットワークの普遍的に見られる特徴的な構造は、それぞれ固有のダイナミクスの結果、最終的に実現したものと考えることができます。
このような不変的構造（システムが変わっても共通に見られる数理構造）は、背後に対応する共通の数理モデルが存在し、それを見つけ出し解析することで、新たな切り口で理論的に理解できる可能性を示唆しています。
あるクラスのネットワーク状に繋がった現実の系は、ダイナミックな素子が互いの結合構造を変化させながら発展するネットワーク結合力学系と見なせます。
一例として神経ネットワークを考えると、ニューロンという基本的要素が互いにシナプス結合を通じて相互作用することにより高度な知能を発現しています。
ここで肝要な点は、ネットワーク構造に依存して各要素の状態がダイナミカルに決まり、一方で各要素の状態に応じてネットワークの結合構造が変化することです。基本的要素自体に固有のダイナミクスがあり、それらの結合ネットワークが要素の状態と共に変化することで、最終的に高度な機能や柔軟な適応能力を発揮すると言えるでしょう。
その本質的なメカニズムを解明することは、絶えず変化する環境に柔軟に対応し、障害に強い安定したシステムを設計する上でも役に立つことが期待できます。
我々は、やや抽象的ですが、変化するネットワーク構造とその上のダイナミクスの一般的性質をネットワーク結合力学系という立場から、分野横断的に共通する不変な性質を明らかにしようとしています。
さらに詳しい説明はここをご覧下さい。
 教授 青柳 富誌生 |
|
|
|