Rhythm is a class of fundamental periodic phenomena found widely not only in physical systems but also in the behavior of living systems and human societies. Particularly, in dissipative dynamical systems, a kind of rhythm behavior referred to as “limit cycle oscillation” often appears as a result of the processes through which energy is absorbed from the external world and then dissipated within the system.
The special characteristic of this kind of rhythm is that for a given system, both the appearance and characteristics of the oscillation are independent of the initial conditions.In other words, this type of asymptotic behavior is robust with respect to external perturbations. It is perhaps for this reason that such behavior is widely observed in living systems, in such diverse forms as circadian rhythm and walking motion.
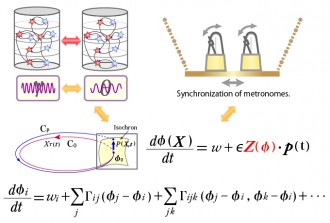
A type of related phenomenon that has been broadly studied both experimentally and theoretically is that in which a system consisting of many elements that each exhibits a different type of rhythm undergoes an entrainment transition to a state in which these elements all exhibit the same rhythmic behavior.
For example, it has been observed that if two pendulum clocks are hung from the same wall, the oscillations of the two pendulums will often become synchronized. This phenomenon can be understood as resulting form the interaction between the two pendulums communicated through the wall (for example, in the form of mechanical vibrations).
The important point here is that although the wall acts as the medium through which the interaction takes place, the appearance of the synchronization is independent of the precise nature of the wall and the manner in which it communicates the interaction. Rather, as long as there exists such a medium to convey the interaction, this synchronization behavior is seen to appear in the same manner for a broad range of such systems.
Because entrainment behavior is observed in a very large variety of systems and it possesses a kind of universal structure that is independent of system details, one would expect that it can be treated generally, from a unified theoretical point of view. In fact, there exists a well-established theoretical framework for treating such systems, the phase reduction (or phase oscillator analysis) method. This framework has been applied to the description of systems in fields ranging from ecology to neurophysiology and physics. It provides a powerful tool for the investigation of non-linear phenomena of many kinds.
We are presently engaged in a wide range of research regarding rhythm synchronization phenomena, from theoretical analyses to the formulation of experimental techniques. Specifically, we are collaborating with other researchers to study synchronization in neuronal systems (periodic neuronal activity, EEGs, etc..), walking motion of robots and various types of rhythmic behavior exhibited human beings.
 Associate Professor Toshio Aoyagi |
|
|
|