「モンテカルロ法」

自然から社会まで様々な分野のシミュレーションやAI等の情報処理にも用いられる確率的数値計算手法。

はじめに

沢山のものが集まった物理的システムは古くから統計物理学の研究対象となってきました。そこで発展してきたモンテカルロ法は、現在、ものだけなく事の集まりである情報システムも含めて、幅広い対象に対する強力なツールとして用いられています。

期待値のモンテカルロ計算

システムが状態\(X\)になる確率を\(P(X)\)とする。その場合、状態\(X\)に依存する量 \(f(X)\)の期待値\(\langle f(X) \rangle\)は次式で定義される。[1]: \begin{equation} \langle f(X) \rangle \equiv \sum_X f(X) P(X) \quad \mbox{又は} ~ \int dX\ f(X) P(X), \end{equation} ここで、後者は状態変数\(X\)が連続変数だった場合を表す。

状態の総数が少ない場合は全ての\(X\)について\(f(X) P(X)\)を足し上げる事で計算することができるが、例えば、\(X\)が\((x_1, x_2, ..., x_D)\)のような多成分の場合、多重和となり全列挙による計算は困難になる。 \begin{eqnarray} \langle f(X) \rangle \equiv & \sum_{x_1}\cdots\sum_{x_D} f(x_1, \dots, x_D) P(x_1, \dots, x_D),\\ \mbox{又は} \equiv & \int \cdots \int dx_1 \dots dx_D\ f(x_1, \dots, x_D) P(x_1, \dots, x_D). \end{eqnarray} 実際、各\(X_i\)が\(K\)種類の値を取りうる時、状態総数は\(K^D\)となり、多重度\(D\)に対して指数関数的に増加する。連続変数の場合も同様である。例えば、\(D\)重積分の場合、それぞれの積分区間を\(K\)個ずつに分割すると積分領域は\(K^D\)個の積分要素に分割される。これは多重度\(D\)に対して指数関数的に大きくなるため、その全列挙は困難である。従って、多重度が大きな場合、全列挙しない方法が必要である。

元々、各状態\(X\)が出現する確率が\(P(X)\)として与えられていたので、素朴に、確率\(P(X)\)に従って生成されたサンプル集団\(\{X_t\}\)の平均として、期待値を近似的に求めることができるように思われる。

\begin{equation} \langle f(X) \rangle \approx \frac{1}{M}\sum_{t=1, \dots, M} f(X_t). \end{equation}

このような計算手法を重み付きモンテカルロ法と呼ぶ[2]。

(4)式右辺のサンプル値平均が真の期待値に収束することは容易に示す事ができる。サンプル値平均は確率変数の集合\(\{X_t\}\)によって定義されているのでこれ自身も確率変数と見なす事ができる。従って、その期待値を計算すると次の様になる。 \begin{equation} \left\langle \frac{1}{M}\sum_{t=1, \dots, M} f(X_t) \right\rangle = \frac{1}{M}\sum_{t=1, \dots, M} \langle f(X_t) \rangle = \langle f(X) \rangle. \end{equation} 分散も同様に計算すると、 \begin{equation} \frac{1}{M}\left[\langle f^2(X)\rangle - \langle f(X)\rangle^2\right] \end{equation} となることがわかる。従って、サンプル数\(M\)が大きな極限で期待値\(\langle f(X) \rangle\)に収束する事が示せた。もう少し正確に言えば、 中心極限定理により、重み付きモンテカルロ法で求めたサンプル平均値が、サンプル数\(M\)が大きい極限で、次の平均と分散をもつガウス分布に収束する事がわかる。

\begin{equation} \mbox{平均}\ \langle f(X) \rangle, ~ \mbox{分散}\ \frac{1}{M}\left[\langle f^2(X)\rangle - \langle f(X)\rangle^2\right]. \end{equation}

この結果からモンテカルロ法の誤差はサンプル数\(M\)が大きくなると\(\frac{1}{\sqrt{M}}\)で減少していくことがわかる。

このように、モンテカルロ法は期待値の近似的な値を出すだけで、その誤差はサンプル数と共に減少していくが速度は早くはない。そのため、メリットがないように思われるが、上で述べたように全列挙が困難な場合、つまり、多重度が高い場合は誤差が多重度によらない事が大きなメリットになる。

これまでは、期待値計算の手法として、モンテカルロ法を紹介してきたが、通常の多重積分や多重和も、適時、確率分布\(P(X)\)に相当するものを設定すれば、モンテカルロ法で計算可能となる。例えば、多重和の状態総数や多重積分の積分範囲の大きさがわかっている場合は、\(P(X)=\)1/(状態総数)、又は、1/(積分範囲の大きさ)に設定することができ、モンテカルロ法で多重和や多重積分が評価できる。

上で述べたように(7)式のガウス分布の分散のルートがモンテカルロ法の精度を意味するが、(7)式自身の評価は通常できない。そこで,（独立な）モンテカルロ計算の平均値の集合\(\{\bar{f}_i\}\)から、近似的に分散を推定することで精度の評価を行うことがしばしば行われる。その場合、期待値の推定値とその精度は次式で与えられる.

\begin{align} &\mbox{推定値}\ \bar{\bar{f}} \equiv \frac{\sum_i \bar{f}_i}{N_M},\nonumber\\ &\mbox{精度} \equiv \sqrt{\frac{\sum_i \left(\bar{f}_i - \bar{\bar{f}}\right)^2}{N_M(N_M-1)}}, \end{align}

ここで、\(N_M\)は独立なモンテカルロ計算\(\{\bar{f}_i\}\)の回数である。

乱数による円周率の計算

以下の積分にモンテカルロ法を適用し、円周率をモンテカルロ法で求める事を考える。

\begin{equation} \int_0^1 dx \ \frac{4}{1+x^2} = \pi. \end{equation}

いま、状態変数を区間\([0,1]\)に属する１次元実数\(X\)と考える。そして、確率密度を\(P(X)=1\)とすれば、円周率を\(\pi = \langle 4/(1+X^2) \rangle\)のように期待値と見なすことができ、モンテカルロ法によって期待値（円周率）を評価する事ができる。しかし、区間\([0,1]\)の一様分布に従うサンプル列\(\{X_t\}\)はどのように生成するのだろうか？

ある区間にでたらめ（一様）に値をとる数を乱数と呼ぶ。乱数同士は定義より独立であるが、ルールに基づいて乱数を作成するとそのような事は原理的にはできない。しかし、実際上、ほぼ独立に見えるような擬似乱数の作り方がいくつか提案されている。例えば、C言語関数xor128は、区間\([0, 2^{32}-1]\)の疑似乱数を作成する[3]。この擬似乱数を区間の長さ(\(2^{32}\))で割る事で、区間\([0,1]\)の一様分布に従う疑似確率変数を作成することができる。現在、擬似乱数の研究は非常に進んでおり、標準的な関数として言語に内包されていたりライブラリー等の形で使用できるのでそれらの利用を勧める。

[1] 例えば、\(f(X)\)は状態が\(X\)の時の対象からの出力値等。また、\(\langle \cdot \rangle\)は統計物理での期待値を表す記号である。

[2]確率に基づく方法であるため、カジノで有名な都市にちなんだ名前が付いている。

[3]本コードはunsigned longが４バイトであるC言語処理系を前提にしている。また、x, y, z, wは種と呼ばれる。ここでは適当な初期値を設定してある.

問題 M1

(1) 円周率を求める為に(9)式の左辺のモンテカルロ計算を行う。サンプル数は\(10, 10^3, 10^5, 10^7\)とした独立な計算を10回おこなうことで、(8)式から各サンプル数での推定値とその精度を報告せよ。

(2) 前問の結果と(7)式と比較し、(8)式の妥当性を検証せよ。

［円周率を表す(9)式のモンテカルロ法によるサンプル平均値の様子］クリックするとサンプル数が変化する。短冊はサンプル値の場所に描かれ、その面積はサンプル平均への寄与分を表す。従って、短冊の総面積がサンプル平均値になっている。

マルコフ連鎖モンテカルロ法

重み付きモンテカルロ法では、確率分布\(P(X)\)に従ったサンプルを作成する方法が必要である。その手法としては、直接的なものとマルコフ過程を用いるものの２種類がある。

与えられた確率分布が指数分布やガウス分布などの低次元の確率分布の場合は、一様分布を使う事で直接的にサンプルを作成することができる。このような手法は、逆関数法や棄却法と呼ばれている。一方、このような単純でない確率分布の場合によく用いられるのが、マルコフ連鎖モンテカルロ法（参考文献[1]）である。

マルコフ過程とその状態の出現頻度の分布

確率過程は状態列を表す確率的モデルの一つで、特に、マルコフ過程は過去の有限ステップの状態にだけ依存して未来の状態が確率的に決定される確率過程として定義される。最もシンプルなマルコフ過程の例は、過去１ステップ分だけに依存する場合である。このようなマルコフ過程では、現在の状態\(X(t)\)に対し未来の状態が\(X(t+1)\)である確率、遷移確率\(P(X(t) \to X(t+1))\)によって定義される。

定義より遷移確率\(P(X \to Y)\)は次の性質を満たす。

\begin{equation} {}^\forall X,\quad \sum_Y P(X \to Y) = 1. \end{equation}

状態空間（全状態から構成される空間）の要素である各状態に番号をつけて\(X_i\)と書く事にして、遷移確率\(P\)から次の遷移行列\(T\)を定義すると便利である: \(T_{ij}\equiv P(X_j \to X_i).\) ここでは、遷移行列\(T\)の成分は非負であるが、特に、\(T^k > 0\)、つまり、全ての成分が正となる整数\(k\)が存在する事を仮定する。この仮定は有限回の遷移でどの状態からスタートしても任意の状態に到達する可能性があると言う事を意味する。\(T^k\)をあたらめて遷移行列とおけば、ペロン・フロベニウスの定理より、遷移行列の最大固有値は1であり対応する固有ベクトルは１つしかなく、更にその成分は全て正、更に、他の固有値は絶対値が1未満である事が示される。今、ステップ\(t\)での各状態を取る確率を成分とするベクトルを\(\mathbf{v}(t)\)とすると、ステップ0からスタートして、ステップ\(t\)のベクトル\(\mathbf{v}(t)\)は次のようになる。 \begin{equation} \mathbf{v}(t) = (T)^t \mathbf{v}(0). \end{equation} 従って、ステップ数を大きくすると固有値1に対応するベクトル\(\mathbf{v}_T\)に収束することがわかる。つまり、マルコフ過程のサンプル列の分布は定常分布\(W_T\) (定義：\(W_T(X_i) \equiv (\mathbf{v}_T)_i\))に収束する。

ベクトル\(\mathbf{v}_T\)の定義式を

\begin{equation} \mathbf{v}_T = T \mathbf{v}_T. \end{equation}

書き換えると、次式（釣り合い条件）になる。

\begin{equation} {}^\forall X, \quad W(X) = \sum_{Y} P(Y \to X) W(Y). \end{equation}

従って、逆にこの式を満たす遷移確率に基づくマルコフ過程から、確率分布\(W\)に従うサンプル列が生成されることがわかる。

(13)式が釣り合い条件と呼ばれる理由は、右辺が状態\(X\)に入ってくる割合、左辺が状態\(X\)から出て行く割合を表すからである（\(\sum_{Y} P(X \to Y) = 1\)より）。もし、状態の出現頻度がこの釣り合いを破っていても、負のフィードバックが働き、釣り合い条件（(13)式）が成立するような頻度に自動的に戻ってくる。例えば、状態\(X\)が出現しすぎているということは、(13)式で確率分布\(W\)を頻度に置き換えた時に左辺が大きいということになっている。そのような時は出て行く割合の方が大きくなるので、最終的に釣り合いがとれる方向に状態\(X\)の頻度が減少して行く。

メトロポリス・ヘイスティングス法、ギブスサンプリング

釣り合い条件(13)式を満たす遷移確率は一つだけではない。実際、さまざまな手法が提案されている。代表的なものがメトロポリス・ヘイスティングス法（メトロポリス法）やギブスサンプリング（熱浴法）である。以下では、それぞれを物理での名称であるメトロポリス法、熱浴法と呼ぶ。それぞれの手順は以下の通りである[4]。

メトロポリス法の手順

手順1.: 初期状態\(X(0)\)を与え、以下の手順で状態列を更新。
手順2.: 現状態を\(X(t)\)とし、次状態候補\(X'\)を確率分布\(Q(X(t),X')\)に従って作成。ただし、簡単化の為、確率分布\(Q(X,Y)\)は対称と仮定する: \(Q(X,Y) = Q(Y, X).\)
手順3.: 次状態候補\(X'\)を確率\(\min\left[1, \frac{W(X')}{W(X(t))}\right]\)で次の状態（\(X(t+1)\equiv X'\)）とし、そうでなければ、現在の状態\(X(t)\)を次の状態（\(X(t+1) \equiv X(t)\)）とする[5]。
手順4.: 手順2に戻る。

熱浴法の手順

手順1.: 初期状態\(X(0)\)を与え、以下の手順で状態列を更新。
手順2.: 現状態\(X(t)=(x_1, x_2, \cdots)\)を構成する状態変数から１つをランダムに選ぶ。例えば、\(x_i\)を選んだとすると、この\(i\)番目の状態変数だけを更新する（それ以外はそのまま）。その際、更新後の値\(x_i^\prime\)を以下の確率にしたがって決定する[5]。 \begin{equation} P(x_i^\prime) = \frac{W(x_1, \cdots, x_i^\prime, \cdots)}{\sum_{x_i}W(x_1, \cdots, x_i, \cdots)} \end{equation}
手順3.: 手順2に戻る。

問題 M2

(1) メトロポリス法の遷移確率が次の詳細釣り合い条件を満たす事を証明せよ。

\begin{equation} \label{eq:dbc} P(X \to Y) W(X) = P(Y \to X) W(Y). \end{equation}

(2) 熱浴法の遷移確率が詳細釣り合い条件を満たす事を証明せよ。

(3) 遷移確率が詳細釣り合い条件（(15)式）を満たす場合は、釣り合い条件（(13)式）が成立する事を証明せよ。

マルコフ連鎖モンテカルロ法で注意すべき点

マルコフ過程を用いてサンプルを生成するとき、各サンプルは過去のサンプルに依存して確率的に生成されてきたので、当然、サンプル同士に統計的な相関がある。通常、有限個しかサンプルは生成できないので、相関が強い場合は、実質的な独立なサンプル数が少なくなる。(7)式の分散の分母は統計的に独立なサンプル数なので、モンテカルロ計算の精度は相関が強くなると悪くなる。その為、相関の強さを確認しながら計算を進めることが必要である。もちろん、相関を弱める手法の研究も進んでいる[6]。

[4] ここでは説明の為に設定を簡略化してある。

[5] 確率分布の比だけしか必要ないのもメトロポリス法や熱浴法の特徴である。

[6] 一般的にはレプリカ交換法などのアンサンブルを拡張するタイプの方法がいくつか提案されている（参考文献[1]参照）。

イジングモデル

統計物理は多数の要素からなる系の性質を対象とする物理学の理論の１つである。ボルツマンなど多くの研究者により、特に平衡系の性質に対する強力な理論が構築されている。その成果は、近年、物理現象だけではなく、ニューラルネットワークやネットワークコミュニティーなど、多数の要素がなる一般的なシステムの解析にも応用され、様々な分野で活用されている。

統計物理での重要な概念の理解には理論モデルが有用である。その中でもイジングモデルは各要素が相互に影響する最も基本的なモデルであり、統計物理では極めて重要なモデルとなっている。また、近年注目されている機械学習分野でもボルツマンマシンと呼ばれ基礎的な計算モデルとして用いられている。以下では、イジングモデルのシミュレーションにマルコフ連鎖モンテカルロ法を適用する方法についてのべる。

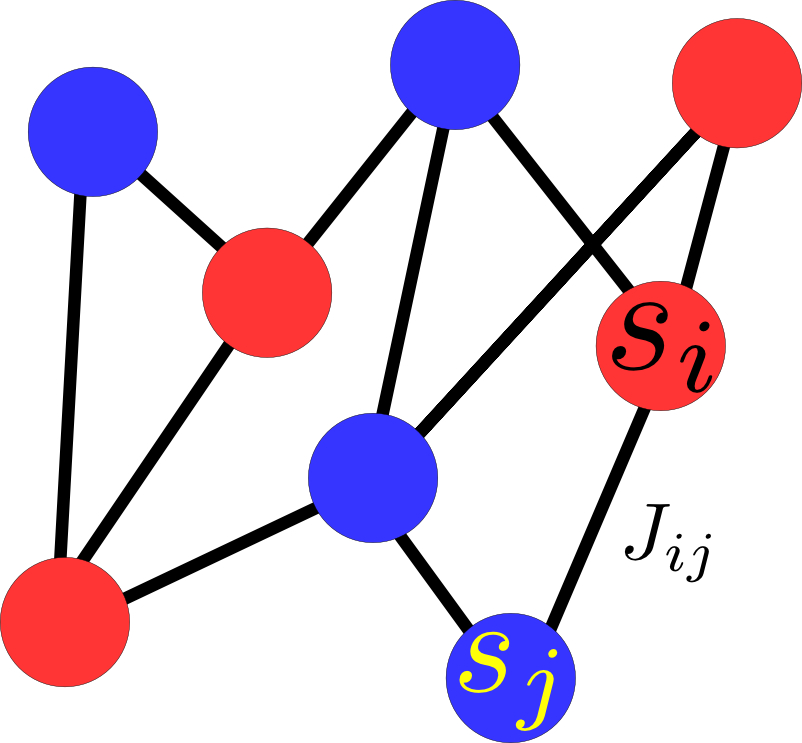
エネルギー

イジングモデルは多数の素子から構成されるシステムである。各素子の状態を表す変数を\(s_i\)は、\(\pm 1\)の値のどちらかをとる。そして、システムのエネルギー\(E\)は以下の形の相互作用の総和になっている。 \begin{equation} E(S) \equiv -\sum_{i,j} J_{ij} s_i s_j \end{equation} ここで、\(J_{ij}\)は相互作用の強さを決める相互作用係数である。

統計物理の理論によると、周りの環境とのエネルギーのやりとりがあると、システムの状態\(S=\{s_i\}\)は環境の温度\(T\)によって支配される次のボルツマン分布に従う。 \begin{equation} P(S) \equiv \exp(-E(S)/T) / Z \end{equation} ここで、\(Z\)は規格化因子で、\(Z=\sum_S \exp(-E(S)/T)\)。また、ボルツマン定数は簡単化の為に省略している。したがって、状態変数による物理量\(A\)の期待値は以下の式で定義される。 \begin{equation} A(T) \equiv \sum_S A(S) P(S) = \sum_S A(S) \exp(-E(S)/T) / Z \equiv \langle A(S) \rangle \end{equation} ここでは、記号\(\langle . \rangle\)は、統計物理で用いられる期待値を表す記法である。

トーラス上のイジングモデルの相転移現象（臨界現象）

一般的に、要素数が無限大の極限（熱力学的極限）では、システムのコントロールパラメータ（イジングモデルでは温度）を変えると、システム全体の性質が突然切り替わる現象が現れる。システム全体の性質が本質的に同じである領域を相と呼び、それが突然、切り替わるこの現象を相転移現象と呼ぶ。イジングモデルの研究により、特に、相転移現象の１種である臨界現象に関する理解が非常に進んだ。２次元イジングモデルは臨界現象を示す最も簡単なモデルとして重要である。

対称性の自発的破れ

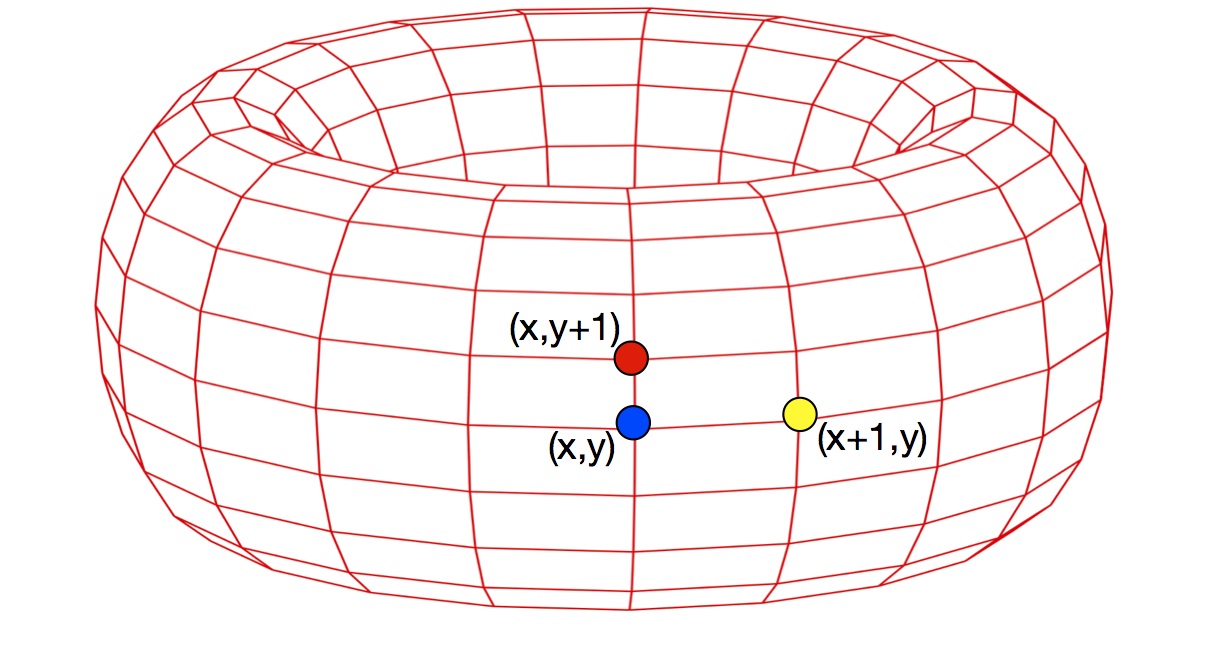
ドーナツ形状（トーラス）の表面に貼付けたグリッドを考える。グリッドの格子点の座標を\((x,y)\) \((0 \le x, y \le (L-1))\)とすると、ドーナツ形状より格子点\((L,y)\)は\((0,y)\)と、\((x,L)\)は\((x,0)\)と同一点になる（周期的境界条件）。この各格子点にイジング素子（イジングスピン）が１つづつあり、前後左右とだけ相互作用をしているとする。特に相互作用定数\(J\)が全て同じで1である場合は２次元強磁性イジングモデルと呼ばれる。

強磁性イジングモデルは全てのイジングスピンの符号を反転させてもエネルギーが変わらないという対称性をもつ。エネルギーが変わらないのでボルツマン分布による状態の出現確率は全反転でも同じである。つまり、ある状態とそれを全反転した状態は同じ確率で出現する。一方で、温度を下げていくと、エネルギーが低い状態の出現確率がボルツマン分布の式から上がることがわかる。したがって、温度が非常に低くなると、全てのイジングスピンが同符号になる状態が出現することになる。しかも、上に述べたように、対称性があるので、そのような状態は２つある。

しかし、環境とのエネルギーのやりとりは局所的である為、状態の変更は局所的にしかおきず、全反転するような状態に変化する為には途中にエネルギーが大きなところを通る必要がある。その為、低温では片方の状態からもう片方の状態に遷移することはほぼ起きない。このようにもともとあった対称性が勝手に破れたような現象を自発的対称性の破れという。実際、２次元イジングモデルは、熱力学的極限である温度以下で自発的対称性の破れが起きることが証明されている。

自発的な対称性の破れをみる為に磁化\(m\)と呼ばれる以下の物理量を考える。 \begin{equation} m =\frac{1}{N} \left\vert \sum_i s_i\right\vert \end{equation} ここで、\(\vert \cdot \vert\)は絶対値を表し、\(N\)はイジングスピン数を表す。有限系では対称性より絶対値をつけない場合はこの量の期待値は常に０になるが、絶対値をつけることで揃ったイジングスピンが多い場合は大きくなるので、対称性の破れを有限系でも見ることができる。

モンテカルロシミュレーション

磁化の期待値の計算には多重和を取る必要がある。しかし、その組み合わせの数は\(2^N\)と膨大であることから、厳密に和を取ることは難しい。そこでモンテカルロ法がよく用いられる。ただ、確率\(P(S)\)で状態\(S\)を直接サンプリングすることは、ボルツマン分布の形が複雑なため不可能である。そこで、マルコフ連鎖モンテカルロ法がよく用いられる。

マルコフ連鎖モンテカル法として、前章では、メトロポリス法と熱浴法を紹介した。どちらも適用可能である。例えば、メトロポリス法を適用した場合、次のような手順になる。

イジングモデルのメトロポリス法

以下の手順（1 Monte Carlo Sweep(MCS)と呼ぶ）で次の状態\(S(t+1)\)を確率的に作成する。

手順1.: ランダムに格子点を１つ選ぶ。
手順2.: 選んだ格子点の状態変数\(s\)をフリップしたものを次状態候補\(s^\prime\)とする。フリップとは、\(s=1\)なら\(-1\)に、またはその逆の操作を意味する。
手順3.: 区間[0,1]の一様乱数\(r\)を作成し、もし、 \begin{equation} r \le \min\left[1, \frac{P(\cdots, s^\prime, \cdots)}{P(\cdots, s, \cdots)}\right] \end{equation} ならば\(s\)をフリップする。それ以外は何もしない。
手順4.: 以上の手順を総格子点数の回数だけ行う。

ここでは、手順２でランダムに格子点を選んだが、これを格子を規則的に１巡するものに置き換えても良い。例えば、端から順番に更新しても良い。この場合も、格子を一巡（1MCS）するごとに、状態を見れば、詳細釣り合いを満たすからである。

問題 M3

トーラス上の強磁性イジングモデル\(J=1\)を考える。システムサイズは\(L\times L\)とする。

(1) イジングモデルの熱浴法の手順を書け。

(2) マルコフ連鎖モンテカルロ法のサンプル列内の相関を見る為に、初期状態の影響が消える様子をグラフを用いて示せ。観察する量は各ステップでの磁化。ただし、温度は\(z=\exp(2/T)-1=\sqrt{2}\)、システムサイズは\(L=64\)とし、初期状態\(S(t=0)\)は全てのイジングスピンが1とする。特に、メトロポリス法、熱浴法それぞれでシミュレーションを行い、それらの結果を比較すること。

(3) 磁化の期待値について、温度とシステムサイズへの依存性をモンテカルロ法により求めて報告せよ。ただし、\(z\)は区間\((1.2, 1.5]\)内に均等に\(12\)点以上、システムサイズは\(L=12, 16, 24, 32, 48, 64\)とし、各モンテカルロ計算でのサンプリング数はトータルで\(10^6\)MCS以上（例: \(10^5\)MCSを\(10\)セット）とする。また、初期値の影響が残らないように、問題(2)の結果を参考に、最初の（十分な）ステップを平均値の計算には含めないようにすること。

(4) (3)の計算結果に基づき、システムサイズが大きくなった極限での磁化の割合の振る舞いを議論せよ。

［強磁性イジングモデルのメトロポリス法によるモンテカルロシミュレーション］画面クリックにより\(z\)値の再設定と100MCSを行う。上部グリッドに状態\(s(r)\)（システムサイズは32 x 32）を２色で、更に、その下に\(z\)の設定を表示。新しい\(z\)値はクリック時のポインターの水平座標で決定され、その対応関係は一番下のメーターバーの赤部分で表示。

おわりに

本ページは数値計算手法としてのモンテカルロ法のさまざまな性質については証明などはせず、簡単に紹介しただけになっている。例えば、収束性などについて詳しく知りたい場合は、例えば、参考文献[1]を参考にされたい。

また、準備の関係上、取り上げなかったアルゴリズムももちろん多々ある。特に、マルコフ連鎖モンテカルロ法に関して、連続変数でサンプル空間が定義されている場合のハイブリッドモンテカルロ法、サンプリングが困難な場合によく用いられる拡張アンサンブル法（レプリカ交換等）を取り上げなかった。後者については、参考に最近の講義録（参考文献[2]）を上げておく。

冒頭に述べたように、モンテカルロ法は多数の要素からなる確率的なシステムの研究には欠かせないものとなっている。このような多数の要素からなるシステムは物理では多体系と呼ばれ、素粒子から物質の研究までをスケールを超える研究対象となっている。計算手法のモンテカルロ法だけなく、背後にある多体系に関するアンダーソン博士の More is different の気持ちを多くの人に知っていただければと思う（参考文献[3]）。

参考文献

伊庭幸人, 種村正美, 大森裕浩, 和合肇, 佐藤整尚, 高橋明彦：計算統計II マルコフ連鎖モンテカルロ法とその周辺 (統計科学のフロンティア 12), 岩波書店 (2005年).
福島孝治, モンテカルロ法の基礎と応用計算物理学からデータ駆動科学へ, 物性研究・電子版, Vol.7, No.2. 072214 (2018年).
一般書籍「数理工学の世界」第3章「沢山からできている世界」, 日本評論社, 2019年10月25日第1刷発行, ISBN 978-4-535-78883-1.