 脳内の神経細胞が示す周期的なスパイク発火、レーザーの発振、心臓の鼓動など、私達の周りで安定して観測されるリズム(振動)現象のほとんどは数学的には非線形振動子として記述されます。振動現象において最も重要な現象の一つが、複数の振動子がタイミング(位相)を揃えて振動する位相同期現象です。位相同期は時間的な自己組織化の代表例であり、化学反応、電子回路、細胞内での代謝反応など極めて多くの応用が知られています。
脳内の神経細胞が示す周期的なスパイク発火、レーザーの発振、心臓の鼓動など、私達の周りで安定して観測されるリズム(振動)現象のほとんどは数学的には非線形振動子として記述されます。振動現象において最も重要な現象の一つが、複数の振動子がタイミング(位相)を揃えて振動する位相同期現象です。位相同期は時間的な自己組織化の代表例であり、化学反応、電子回路、細胞内での代謝反応など極めて多くの応用が知られています。
位相同期は通常、互いに影響を与え合う何らかの結合を持つ非線形振動子間で実現します。ところが互いの間に何のつながりもない独立した振動子間でも、それらを共通のノイズで駆動すれば位相同期を達成することが可能です。この現象は共通ノイズ同期(common noise-induced phase synchronization)と呼ばれています。この現象は、神経細胞の応答を観察した実験から、その存在が知られていましたが、それが神経細胞特有の現象なのか、あるいは他の非線形振動子でも起こり得る一般的な現象なのかは未解明に残されていました。
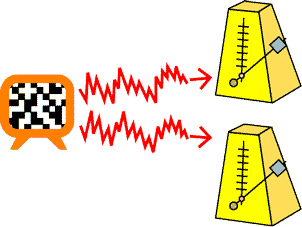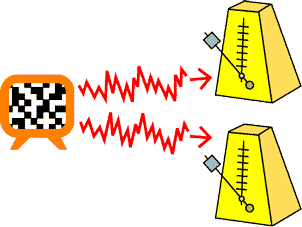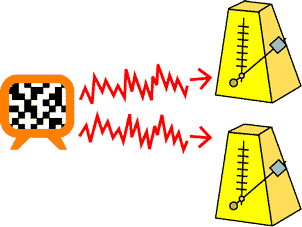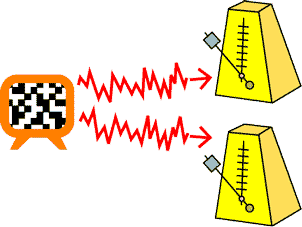 私たちは、位相縮約法(非線形振動子の高次元の時間発展方程式から,一次元の位相の時間発展方程式を導く手法)と確率解析と呼ばれる分野の数学的手法を組み合わせることで、位相同期のメカニズムを数理的に解明することに成功し、その結果、この現象が、どんな非線形振動子でも普遍的に発生することを発見しました。リズムとノイズという、一見すると相反する2つの現象の密接な関連が明らかになったのです。
私たちは、位相縮約法(非線形振動子の高次元の時間発展方程式から,一次元の位相の時間発展方程式を導く手法)と確率解析と呼ばれる分野の数学的手法を組み合わせることで、位相同期のメカニズムを数理的に解明することに成功し、その結果、この現象が、どんな非線形振動子でも普遍的に発生することを発見しました。リズムとノイズという、一見すると相反する2つの現象の密接な関連が明らかになったのです。
このように、非線形性が確率性の結びつきは、様々な非自明な現象を生み出す可能性があります。例えば、私達の脳は、非線形性を利用して確率を制御することで柔軟な情報処理を実現しているように見えます。このような現象をきちんと理解するために、確率性を積極的に取り入れた非線形システムを基礎づける数理的な研究を進めています。
|
|
