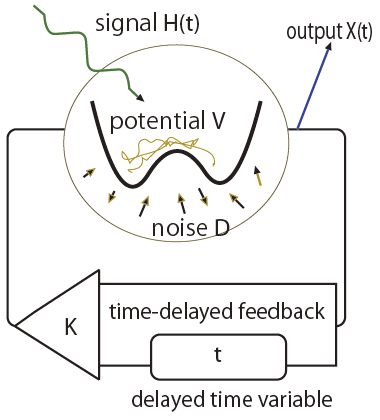
Stochastic resonance is a phenomenon in which the sensitivity of a system to an external signal is increased through the application of noise of a particular strength. This phenomenon has become the subject of many interdisciplinary studies in, for example, biological and nano-scale systems.
In Tutu (2011), as an application of a time-delayed feedback method, we construct a mathematical model that describes the increase in sensitivity resulting from stochastic resonance.
Time-delayed systems are non-Markovian, and for this reason, their treatment is very difficult. To address this difficulty, in Tutu (2011), we employ the finite pole expansion method, which is a self-consistent, systematic computational method. Specifically, we use a two-pole expansion approximation to study a method by which the response function and the correlation function can be analytically computed for non-Markovian systems.
We believe that the development and application of analytical methods for treating non-Markovian stochastic processes will become increasingly important, particularly in the contexts of brain science and nano-scale systems.
 Assistant Professor Hiroki Tutu |
|