ニュートン・コーツ型
積分区間\([a,b]\)を等間隔に分割し、各分割区間上の関数を多項式で近似して積分を求める。多項式は解析的に積分できるので、式(1)の積分公式を構成することができる。区間幅\(h\)は積分区間の分割数\(n\)に対して、\(h=\frac{b-a}{n}\). 多重積分でも同様に各自由度ごとに等間隔に分割し、積分範囲を小領域に分割する。そして、各領域上の関数を多項式で近似し、積分公式を構成することができる。
このように、積分区間を等間隔に分割して、各分割区間上の関数を多項式で近似して、積分を計算する手法の積分公式を、ニュートン・コーツ型積分公式という。
ここでは取り上げないが、分割サイズを等間隔にしないで最適化した場合のガウス型積分公式もよく用いられる。
以下では、1次式、2次式を適用した場合のニュートン・コーツ型積分公式について紹介する。
台形公式
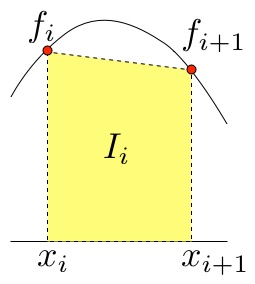
各区間を1次式(直線)で近似すると、 \begin{equation} I_i^{\rm trapezoid} = \frac{h}{2}(f_i + f_{i+1}). \end{equation} 従って、分割数\(n=\frac{b-a}{h}\)とした場合、 \begin{eqnarray} \int_a^b f(x) dx &\approx& \sum_{i=0}^{n-1} I_i^{\rm trapezoid} \qquad (x_i \equiv a + hi)\\ &=& \frac{h}{2}(f_0 + 2 \sum_{i=1}^{n-1} f_i + f_n). \end{eqnarray}
台形公式の誤差
テイラー展開 \(f_{i+1}=f_i+hf_i'+\frac{h^2}{2!}f_i''+\cdots\)より、 \begin{equation} f_i' = \frac{f_{i+1}-f_i}{h} - \frac{h}{2!}f_i''-\cdots. \end{equation} また、一般的に、 \begin{eqnarray} \int_{x_i}^{x_{i+1}} f(x) dx &=& \int_0^h f(x_i+z)dz\nonumber\\ &=& h f_i + \frac{h^2}{2}f_i' + \frac{h^3}{6}f_i''+\cdots \quad (\mbox{テイラー展開式の代入より})\nonumber\\ &=& I_i^{\rm trapezoid} -\frac{h^3}{12}f_i'' -\cdots \end{eqnarray}
よって、誤差の主要項は、\(E_i\equiv \int_{x_i}^{x_{i+1}} f(x) dx - I_i^{\rm trapezoid} = -\frac{h^3}{12}f_i''\).
全体の誤差は、 \begin{equation} E = \sum_{i=0}^{n-1} |E_i| \le \frac{b-a}{12}h^2 M, \end{equation} ただし、\(M = \max_\xi | f''(\xi)| \quad (a \le \xi \le b).\)
誤差のまとめ
- \(h^2\)に比例して、減少。
- \(f''\)が大きい時に、誤差が大きくなる。
シンプソンの公式
区間\([x_{i-1}, x_{i+1}]\)を2次式で近似する。すると、台形公式と同様にテイラー展開を用いて、 \begin{equation} \int_{x_{i-1}}^{x_{i+1}}f(x)dx = \frac{h}{3}(f_{i-1}+4f_i+f_{i+1}) -\frac{h^5}{90}f_i''''+\cdots. \end{equation} よって、 \begin{equation} \int_a^b f(x)dx \approx \frac{h}{3}(f_0+4\sum_{i=1}^{n'} f_{2i-1} + 2\sum_{i=1}^{n'-1} f_{2i} + f_{2n'}), \end{equation} ただし、\(n'=\frac{b-a}{2h}\).
積分区間に無限大を含む場合
積分変数の変数変換を行い、有限区間に積分区間を変換する。
例:
\begin{equation} \int_0^\infty x \exp({-5x^2})dx = \frac{1}{2}\int_0^1 t^4 dt \quad (t = \exp({-x^2})). \end{equation}収束の遅い場合
台形公式やシンプソンの公式どちらも区間内に被積分関数が発散するなど特異点があると、微係数が大きくなり精度が悪くなる。これは事前に変数変換で除くことができる場合もある。
例:
\begin{eqnarray} \int_0^1 \sqrt{1-x^2}dx &=& 2\int_0^1 t^2\sqrt{2-t^2}dt\quad (t^2=1-x)\\ \int_0^1\frac{\exp(-x)}{\sqrt{x}}dx &=& 2\int_0^1\exp(-t^2)dt\quad (t=\sqrt{x})\\ \int_0^1 \frac{dx}{\sqrt{(1-x^2)(1-k^2x^2)}} &=& \int_0^{\frac{\pi}{2}}\frac{d\theta}{\sqrt{1-k^2\sin^2\theta}}\quad(x=\sin\theta). \end{eqnarray}
問題 I1
(1) 以下の定積分の計算に、台形公式を適用し、結果を報告せよ。特に、誤差の主要項の理論的予想と比較せよ。ただし、分割数\(n=10, 10^2, 10^3, 10^4, 10^5\)とする。
(2) 台形公式の時と同様に、シンプソンの公式の主要誤差を導出せよ。
(3) 小問(1)の定積分の計算に、シンプソンの公式を適用し、小問(1)と同様に結果を報告せよ。特に、台形公式との違いも論ぜよ。