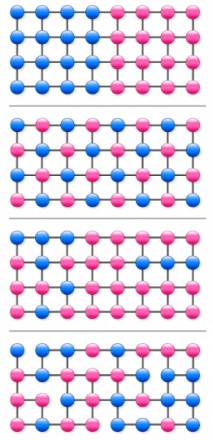
ノードにはノード特性量というものが割り当てられており、この量は時間変動しません。例えば、SNSでの市場調査では、各ユーザの商品への関心の有無、WEB検索の場合では、ある検索語を含むか否かを数値化した0と1であり、図では、![]() や
や![]() で表されています。これは連続的に変化する量でも構いません。
で表されています。これは連続的に変化する量でも構いません。
最初の3つのグラフは正方格子であり、最後のグラフは正方格子から幾つかのリンクを外してあります。3番目と4番目のグラフでは、![]() と
と![]() の配置は同じです。もちろん、これらのグラフのリンク構造やノード特性量の配置は目で見て区別できるわけですが、ノード数が多くなると、リンク構造とノード特性量を同時に捉えることは容易ではありません。
の配置は同じです。もちろん、これらのグラフのリンク構造やノード特性量の配置は目で見て区別できるわけですが、ノード数が多くなると、リンク構造とノード特性量を同時に捉えることは容易ではありません。
これらのグラフの上で、酔歩を行い、酔歩粒子が訪れたノードのノード特性量を並べることにより、ノード特性量のランダムな時系列が得られます。その揺らぎの大偏差統計からリンク構造とノード特性量を同時に特徴づけることを試みましょう。
1番目のグラフでは、0が無限に続く極端な時系列と1が無限に続くもう1つの極端の時系列の間で、0と1がランダムに並ぶ時系列が現れ、ノード特性量のレート関数は0と1の間で下に凸な滑らかな関数であり、長時間平均1/2のところで、極小値0となります。
2番目のグラフでは、どんな酔歩を行っても、0101…という周期的な時系列が現れ、揺らぎはありません。レート関数は点(1/2,0)となります。同じ正方格子でありながら、ノード特性量の配置が異なるだけで、レート関数はこのように極めて異なる形となります。
3番目と4番目はノード特性量の配置は同じですが、リンク構造は異なり、レート関数にも違いが現れます。
次に、左記の2つのグラフを考えましょう。
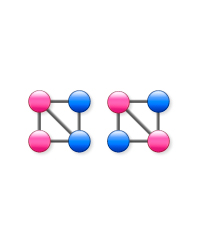 どちらも4ノードの完全グラフから1つ対角線のリンクを外したもので、リンク構造は同一です。しかし、ノード特性量の配置は異なり、揺らぎの性質は異なります。これら2つのグラフを構成する8つのノードの異なる2つのノードのすべての組み合わせについて、非常に弱い無向リンクを張ります。
どちらも4ノードの完全グラフから1つ対角線のリンクを外したもので、リンク構造は同一です。しかし、ノード特性量の配置は異なり、揺らぎの性質は異なります。これら2つのグラフを構成する8つのノードの異なる2つのノードのすべての組み合わせについて、非常に弱い無向リンクを張ります。
このリンク強度をεとし、(—)や(\)で表される元のリンクの強度は1−εとします。
このようにして、構成した8ノードのグラフ上の酔歩で、ノード特性量のレート関数を求めると、ε→0の極限で、二か所で非解析的となり、レート関数はそれを境に三か所の部分からなります。時間変動する量の大偏差統計関数に現れる非解析性はq相転移としてカオス力学系に対して研究がなされています。ここに現れる相は、クライシスのような分岐や非双曲性に起因するアトラクタの特徴的な局所構造に対応します。
グラフ上の酔歩から得られるq相転移の相とは何でしょうか。上記の8ノードの例では、2つの非解析点で挟まれるレート関数の部分は右の4ノードからなるグラフに対応し、非解析点の外側の2つの部分は左の4ノードからなるグラフに対応します。
従って、この場合の相はノード特性量の配置を含めた特徴的な部分グラフ、あるいは、クラスタといったものに対応します。このような局所構造の抽出にはレート関数のみならず、Gibbsの確率測度に相当する重み付きのノードの訪問頻度が必要となります。GoogleのPageRankは、原理的には、重みのない単純な酔歩による訪問頻度から得られることに注意しておきます。
|