講師のプロフィール
宮崎 修次（みやざき しゅうじ）
京都大学大学院情報学研究科・講師
専門は非線形物理学・非平衡統計力学。
長崎市出身。小学生の頃は天体観測をしたり、天気図を書くのが好きでした。高校生のときは、地学部に所属して、太陽黒点・流星群の観測、気象観測、地質巡検を部員のみんなと楽しんでいました。特にこれといったきっかけはありませんが、いつの間にか、物理学の研究者になっていました。
現在では、いろいろな情報をパソコン、スマホ、携帯電話で検索できますので、物理や数学が好きな人、得意な人に向いた職業にどのようなものがあるのか、高校生のうちから検索してみるとよいと思います。
受講生へのメッセージ
『未来を予測するということ』
昨年の８月１３日深夜から翌日にかけて降り続いた記録的な豪雨により、京都府南部地域豪雨災害が生じ、私が居住している宇治市でも大きな被害が生じました。私はそのときはお盆休みで、出身地の長崎市におりましたが、その長崎も１９８２年７月２３日に長崎大水害を経験し、有名な眼鏡橋が半壊し、３００名近くの方が犠牲になりました。通りかかった崖崩れの現場で小さい女の子の遺体が発見され、泥まみれのパジャマが少しだけ見えたことをはっきり覚えています。このような豪雨災害や大きな地震・津波の発生が正確に予測できたらどんなにすばらしいでしょう。
気象観測で得られる気温などのデータがどのような規則で時間変化をするかを決める物理法則を数式で表現し、コンピュータの助けを借りてそれを解くことで、現在の天気予報が行われています。この実習の大きなテーマである「カオス」の研究の源流の一つは天気予報にあります。
実習で天気予報を行うのは無理ですので、もう少し、簡単な例で、自然現象の予測を行ってみましょう。毎年、農作物や漁獲量がどのように変動するのかは大変重要な問題です。生き物の数の変動の仕方を個体数変動といいます。人間については、人口動態といいます。英語では、population dynamics という同じ言葉を使います。
「八日目の蝉」という小説や映画が話題になりましたが、八日というのは成虫としての短い寿命と関係しており、親の世代と子供の世代が重なりません。このような蝉の個体数変動を考えてみましょう。成虫の雌が多数の卵を産み、その一部が成虫になりますが、ある年の成虫の数と次の年の成虫の数との比を増殖率と呼びましょう。
この増殖率が一定の場合、例えば、増殖率が２のとき、翌年の成虫の数は２倍、その翌年の数は４倍、このように個体数は発散していきます。増殖率が１／２のとき、翌年の成虫の数は１／２、その翌年の数は１／４となり、最終的には絶滅してしまいます。このような個体数変動はマルサス的変動とも言いますが、高校数学では、「等比級数」と関係しています。教材の中には、この等比級数の例題として、利息の計算が挙げられています。ここで、蝉の個体数変動や利息の計算がいったん「等比級数」として共通の数学的な表現されると、「蝉の増殖率」や「利息」という全くことなる量が共通の法則に従って、取り扱えることに注意しましょう。
このような等比級数的な蝉の個体数変動が不自然であることには、すぐに気付きましたね。
蝉は毎年鳴いてくれますし、絶滅することも、個体数が発散することもありません。何が不自然でしょうか。あまり個体数が増えると、個体あたりのえさが減ってしまいますね。そこで、増殖率が一定値ではなく、個体数増えると、増殖率は個体数に比例して減るということにしましょう。
このような個体数変動は等比級数では表現できません。この場合の個体数を時間の関数として表現することはできませんので、コンピュータの助けを借りることにします。現在の天気予報がコンピュータを用いた数値予報であることを思い起こしましょう。
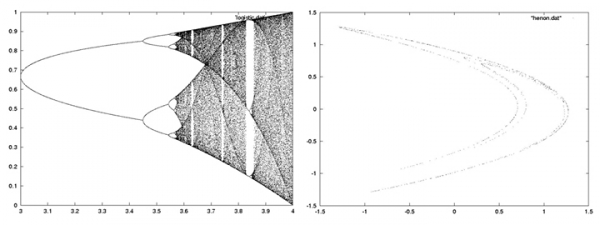実習では、パソコンの表計算ソフトの助けを借りて、このような個体数変動を求め、図示する方法を体験してもらいます。
また、分岐図やアトラクタと呼ばれる右図の図形を書いてもらい、その意味もみなさんで考えて頂きます。
『長さや面積を計るということ』
これらの図形には、一部分が全体と似ているという性質があります。
もう少しわかりやすいブロッコリーの写真を見ましょう。根元からいくつかの茎が分かれていますが、分かれた先の部分の形がもとの全体の形によく似ていることがわかります。このような性質を自己相似性といいます。
実習では、為替相場や株価の時間変化を表すグラフや地震が発生したときの時刻とマグニチュードの関係を表すグラフにこのような自己相似性があることを確かめてもらいます。また、リアス式海岸の長さを地図上で計ってもらいます。滑らかな曲線を１ｃｍの棒でなぞるときの本数は５ｃｍの棒でなぞるときの本数の約５倍になりますが、自己相似性を持ち、入り組んだ曲線の場合はどうなるでしょうか。図の日本地図は小さい犬の顔を並べてできています。顔の面積とその個数で日本のおよその面積がわかります。複雑に入り組んだ自己相似性を持つ図形の面積はどうなるでしょうか。実習では、長さや面積をはかることの意味を少し詳しく考えてみることにします。
『全体と部分 —重ね合わせでは説明できない非線形現象—』
カオス研究の源流の一つが天気予報にあると前に述べました。雲が浮かび、雨や雪が降る気象現象の舞台は地表のごく近くの対流圏です。対流は流体や気体が移動することで全体の温度を一様にしようとする運動です。気象現象のみならず、料理で加熱している鍋の中などいろいろなところで生じます。そこで、ホットプレートに熱をよく伝えるアルミ製のシャーレをのせて、水や油を加熱する実験を行います。このままでは対流の様子がわかりませんので、ポスターカラーや油絵の具を少量投入してみます。どのようなことが起こるでしょうか。
鍋の中の対流の大きさは鍋の大きさとほぼ同じですが、対流を起こしている水を構成している水分子は無数にあり、その水分子どうしが影響を及ぼし合っています。仮に、個々の水分子の運動を観測できたとしても、対流運動を説明するのは不可能といってよいといいでしょう。多数の構成要素が、単純な重ね合わせとして説明できないような影響の及ぼし合いを行っているとき、要素個々の運動からはわからない、質的に新しい全体の運動が生じることがよく起こります。非線形現象ともいいます。この要素というのは原子や分子といった非常に小さいものである必要はありません。ロンドンにミレミアムブリッジができて、大勢の人が渡り初めを行ったときに大きな振動現象が生じ、工事をやり直したことがあります。このときの構成要素は橋の上の歩行者です。そこで、これに近い現象を経験してもらうために、二つの振り子型のメトロノームを、紐でつるして横方向に揺れることができる台の上にのせて、メトロノームを振らせます。二つのメトロノームのテンポを少しずらした場合、どのようなことが起こるか確認しましょう。また、三台以上のメトロノームをのせた場合も試してみましょう。
プラズマという言葉は、テレビや空気清浄機のような家電製品の製品名や機能として聞いたことがあるかもしれません。水蒸気の中の水分子は水素原子、酸素原子、電子が強く結びついていますが、プラズマでは原子や電子がばらばらになった（電離した）状態で、固体、液体、気体の物質の三態とは異なる状態です。雷、蛍光灯、オーロラなどいろいろなところで現れます。雷は一本のキザギザな線に見えますが、高速度カメラでとらえると前の項目で述べた自己相似性を持っています。プラズマと関連した現象には、部分の重ね合わせで説明のできないものが数多く存在します。そこで、プラズマボールという一般に売り出されている玩具で遊んでみます。また、みなさんに電子レンジで実際にプラズマ火球を作ってもらいます。陶磁器の皿に砂か土を薄く撒いて、その上にシャープペンシルの芯を一本のせます。これにガラス製のコップをかぶせて、電子レンジの中に入れて作動させます。何が起こるでしょうか。高熱で溶けるので、コップも皿もプラスティック製のものは使えません。
短い時間ですが、一見難しそうに見えるカオス、フラクタル、非線形の世界の一端を楽しみながら感じて頂ければ幸いです。
宮崎 修次
- 中高生向け研究室公開行事 TOPに戻る
- 中高生向け研究室公開行事｜著作権について